خصوصیات الگوی مثلث
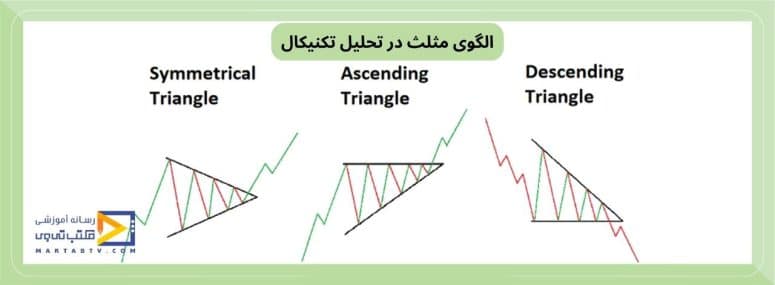
الگوی مثلث یکی از مفاهیم پایهای در هندسه است که در بسیاری از مسائل ریاضی و علمی کاربرد دارد. این الگو به دلیل ویژگیهای خاص خود، در تحلیل و حل مسائل مختلف نقش مهمی ایفا میکند. فهم درست خصوصیات آن میتواند به درک عمیقتری از ساختارهای هندسی و کاربردهای آنها منتهی شود.
در این مقاله به بررسی خصوصیات الگوی مثلث خواهیم پرداخت. با تمرکز بر ویژگیهای هندسی، شناسایی انواع مختلف مثلثها و نحوه کاربرد آنها، میتوانیم به روشنی به جنبههای مختلف این شکل هندسی پی ببریم. این خصوصیات در زمینههای گوناگونی مانند معماری، طراحی، و حتی علم مهندسی مورد استفاده قرار میگیرند.
همچنین، توجه به تفاوتها و شباهتهای موجود بین انواع مثلثها، به ویژه در کاربردهای خاص، از جمله مسائلی است که در این مقاله مورد بررسی قرار خواهد گرفت. برای درک بهتر این مفاهیم، به ویژگیهایی همچون اندازه زوایا، طول اضلاع و روابط میان آنها خواهیم پرداخت. این موضوعات به فهم دقیقتر و کاربردیتر هندسه مثلثها کمک خواهد کرد.
مفهوم مثلث در هندسه
مثلث یکی از اشکال پایهای هندسه است که در بسیاری از ساختارهای هندسی و ریاضی دیده میشود. این شکل با داشتن سه ضلع و سه زاویه، به عنوان یک واحد ساختاری اساسی در هندسه شناخته میشود. درک مفهوم مثلث به درک بسیاری از روابط هندسی و ریاضی کمک میکند و پایهگذار مفاهیم پیچیدهتری است که در سطوح بالاتر ریاضیات بررسی میشود.
در هندسه، مثلثها به دلیل ویژگیهای خاص خود، همچون روابط میان اضلاع و زوایا، نقش مهمی در حل مسائل مختلف ایفا میکنند. مفهوم مثلث به طور کلی به بررسی شکلهایی پرداخته میشود که با تغییر در اندازه و زاویهها، خواص متفاوتی از خود نشان میدهند. این ویژگیها میتوانند به درک بهتر نحوه عملکرد اشکال هندسی در فضا و کاربردهای عملی آنها کمک کنند.
انواع مثلثها و ویژگیهای آنها
مثلثها به عنوان یکی از اشکال هندسی پایه، بر اساس ویژگیهای مختلفی طبقهبندی میشوند. این طبقهبندیها بر اساس اندازه زوایا و طول اضلاع صورت میگیرند. هر نوع مثلث ویژگیهای خاص خود را دارد که در تحلیل مسائل هندسی و ریاضی نقش مهمی ایفا میکند. شناخت انواع مثلثها و تفاوتهای آنها به درک بهتر ساختار هندسی فضا کمک میکند.
مثلثهای بر اساس اندازه زوایا
مثلثها بر اساس زوایای داخلی خود به سه نوع مختلف تقسیم میشوند. در مثلثهای مختلف، زاویهها و خصوصیات هندسی آنها به گونهای است که هر کدام ویژگیهای خاصی دارند که در بسیاری از مسائل کاربردی مورد استفاده قرار میگیرند.
مثلثهای بر اساس طول اضلاع
از نظر طول اضلاع، مثلثها به سه دسته مختلف تقسیم میشوند. این دستهبندی به طور مستقیم بر روی خواص هندسی مثلثها تأثیر میگذارد و در حل بسیاری از مسائل هندسی بسیار مفید است. از جمله ویژگیهایی که در این دستهبندی مورد توجه قرار میگیرد، میتوان به تقارن و روابط ریاضی میان اضلاع اشاره کرد.
خواص هندسی مثلث متساویالساقین
مثلث متساویالساقین یکی از انواع مثلثها است که ویژگیهای هندسی خاصی دارد. این ویژگیها باعث میشوند که این نوع مثلث در مسائل مختلف هندسی و ریاضی کاربرد ویژهای داشته باشد. خصوصیات خاصی چون تقارن و روابط میان اضلاع و زوایا در این نوع مثلثها شناسایی و بررسی میشود که در تحلیل و حل مسائل پیچیده مؤثر است.
تقارن در مثلث متساویالساقین
یکی از ویژگیهای برجسته مثلث متساویالساقین، تقارن آن است. در این مثلث، دو ضلع برابر موجب میشوند که این مثلث نسبت به خطی که از راس زاویه باز به وسط قاعده کشیده میشود، تقارن داشته باشد. این خط را محور تقارن مینامند و هر نقطهای از مثلث که در یک طرف این محور قرار دارد، معادل نقطهای در طرف مقابل آن است.
رابطه بین زوایا و اضلاع در مثلث متساویالساقین
در مثلث متساویالساقین، زاویههای پایه که در دو طرف قاعده قرار دارند، با یکدیگر برابر هستند. این خاصیت باعث میشود که روابط میان اضلاع و زوایا در این مثلث به سادگی قابل محاسبه باشد. به طور کلی، این ویژگیها در حل مسائل مربوط به مثلثها و سایر اشکال هندسی بسیار کاربردی هستند.
مقایسه مثلث قائمالزاویه با دیگر مثلثها
مثلث قائمالزاویه یکی از انواع مثلثها است که ویژگیهای خاصی دارد که آن را از دیگر مثلثها متمایز میکند. این ویژگیها به خصوص در کاربردهای ریاضی و مهندسی بسیار مهم هستند. مقایسه مثلث قائمالزاویه با دیگر انواع مثلثها به ما کمک میکند تا بهتر درک کنیم که هر نوع مثلث در چه زمینههایی بیشترین کاربرد را دارد و چه تفاوتهایی با سایر اشکال هندسی دارد.
ویژگیهای خاص مثلث قائمالزاویه
مثلث قائمالزاویه به دلیل داشتن یک زاویه ۹۰ درجه، ویژگیهای خاصی دارد که آن را از دیگر مثلثها متمایز میکند. این ویژگیها عبارتند از:
- وجود یک زاویه قائم (۹۰ درجه)، که باعث سادهتر شدن محاسبات هندسی میشود.
- قانون فیثاغورس، که ارتباط میان اضلاع مثلث قائمالزاویه را توضیح میدهد.
- وجود روابط خاص میان ضلعهای مجاور به زاویه قائم و وتر مثلث.
تفاوتهای مثلث قائمالزاویه با دیگر مثلثها
در مقایسه با سایر انواع مثلثها، مثلث قائمالزاویه ویژگیهای متفاوتی دارد. این تفاوتها به صورت زیر قابل مشاهده است:
- در مثلثهای متساویالساقین، اضلاع برابر و زوایای پایه برابر هستند، در حالی که در مثلث قائمالزاویه این ویژگیها وجود ندارد.
- در مثلثهای مختلف، معمولاً هیچ زاویهای ۹۰ درجه نیست، اما در مثلث قائمالزاویه یکی از زوایا همیشه ۹۰ درجه است.
- در مثلثهای عادی، روابط سادهای بین اضلاع و زوایا وجود ندارد، اما در مثلث قائمالزاویه، قانون فیثاغورس امکان محاسبه دقیق اضلاع را فراهم میآورد.
کاربرد مثلثها در طراحی و معماری
مثلثها به دلیل ویژگیهای هندسی خاص خود در بسیاری از زمینهها، به ویژه در طراحی و معماری، کاربردهای فراوانی دارند. این اشکال هندسی با استفاده از اصول ساده و در عین حال مؤثر، در ایجاد سازهها، طرحهای معماری و حتی دکوراسیون داخلی نقش اساسی ایفا میکنند. به دلیل تقارن، پایداری و توانایی در انتقال نیروها، مثلثها اغلب در ساختارهای مستحکم و پایدار استفاده میشوند.
در معماری، مثلثها به عنوان عناصر کلیدی در طراحی سازهها و سیستمهای پشتیبانی شناخته میشوند. این اشکال میتوانند در طراحی سقفها، پلها، نمای ساختمانها و دیگر قسمتهای ساختاری مورد استفاده قرار گیرند. علاوه بر این، مثلثها در طراحیهای هنری و دکوراتیو نیز به کار میروند، جایی که زیباییشناسی و کارایی با هم ترکیب میشوند.
| کاربرد | مثال |
|---|---|
| استفاده در ساختارهای سقف | سقفهای هرمگونه و مثلثی در ساختمانهای مدرن |
| تقویت سازههای پل | استفاده از مثلثها در پلهای معلق و قوسی |
| طراحی نمای ساختمانها | استفاده از مثلثها در نماهای هندسی و مدرن |
| دکوراسیون داخلی | استفاده از مثلثها در طراحی مبلمان و تزئینات داخلی |
چرا مثلثها در ریاضیات اهمیت دارند؟
مثلثها یکی از اصلیترین اشکال هندسی هستند که در ریاضیات نقش بسیار مهمی ایفا میکنند. این اشکال ساده اما قدرتمند، در حل مسائل پیچیده ریاضی و هندسی کاربرد دارند و به عنوان ابزارهایی برای تحلیل روابط مختلف بین اجسام هندسی استفاده میشوند. شناخت ویژگیها و خواص مثلثها میتواند به درک عمیقتری از مفاهیم ریاضی کمک کند و پایهگذار حل بسیاری از مسائل علمی باشد.
نقش مثلثها در حل مسائل هندسی
مثلثها در هندسه به دلیل ویژگیهایی چون تقارن و روابط ساده میان اضلاع و زوایا، برای تحلیل و حل مسائل هندسی بسیار مفید هستند. این ویژگیها امکان بررسی دقیقتر اشکال پیچیدهتر را فراهم میآورد. برخی از کاربردهای مثلثها در هندسه عبارتند از:
- محاسبه مساحت مثلثها و سایر اشکال هندسی مرتبط.
- استفاده از قانون فیثاغورس برای محاسبه اضلاع در مثلثهای قائمالزاویه.
- کاربرد مثلثها در تحلیل روابط هندسی پیچیدهتر و ساختارهای فضایی.
مثلثها در ریاضیات کاربردی
مثلثها نه تنها در هندسه، بلکه در سایر شاخههای ریاضیات و علوم کاربردی نیز اهمیت دارند. در مباحثی چون مثلثات و آنالیز، مثلثها ابزارهای اصلی برای حل مسائل پیچیده ریاضی هستند. کاربردهای مثلثها در این زمینهها شامل موارد زیر است:
- استفاده در تحلیل مثلثات و محاسبه زوایا و اضلاع ناشناخته.
- مدلسازی پدیدههای طبیعی و فنی از طریق روابط هندسی.
- کاربرد در محاسبات فیزیکی و مهندسی، به ویژه در مسائل مربوط به فیزیک و مکانیک.
یک پاسخ بگذارید
دسته بندی
- بهترین بروکرهای فارکس
- مبانی تجارت فارکس
- بازار فارکس در افغانستان
- فارکس اسلامی در افغانستان
- بهترین استراتژی فارکس
- مدرسه ی فارکس
- کسب درآمد آنلاین فارک
- اموزش معامله گری
- ویدئوهای آموزشی فارکس
- چگونه در بورس سود کنیم
- راز تجارت ایمن
- آموزش کار در فارکس
- پلتفرمهای تجاری
- فارکس فروم در ایران
- فارکس رایگان در افغانستان
- ویدیو های آموزشی فارکس