معادله حرکت

• حسن پورشیرازی
• 2025-01-18

معادله حرکت یکی از اصول بنیادی فیزیک است که به توصیف و تحلیل رفتار اجسام متحرک می‌پردازد. این معادله‌ها به ما کمک می‌کنند تا حرکت اجسام را در شرایط مختلف پیش‌بینی کنیم و بر اساس آن نیروهای مؤثر را شبیه‌سازی یا تحلیل کنیم. در واقع، معادله‌های حرکت برای توضیح چگونگی تغییر موقعیت اجسام در فضا و زمان طراحی شده‌اند و در تمامی شاخه‌های فیزیک و مهندسی کاربرد دارند.

با استفاده از این معادلات، می‌توانیم بسیاری از مسائل پیچیده حرکتی را به روشی سیستماتیک حل کنیم. این ابزار ریاضیاتی به طور خاص در تحلیل حرکت اجسام تحت تأثیر نیروها، سرعت‌ها و شتاب‌ها اهمیت زیادی دارند. معادلات حرکت به ما اجازه می‌دهند که حرکات پیچیده‌تر را نیز ساده کرده و به نتایج قابل‌استفاده برسیم.

در این مقاله به بررسی مفاهیم پایه‌ای، انواع معادلات حرکت و کاربردهای آن در دنیای واقعی خواهیم پرداخت. به علاوه، روش‌های مختلف حل این معادلات را نیز مورد بررسی قرار خواهیم داد تا بتوانیم درک بهتری از رفتار اجسام در شرایط مختلف پیدا کنیم.

انواع معادلات حرکت در سیستم‌های مختلف

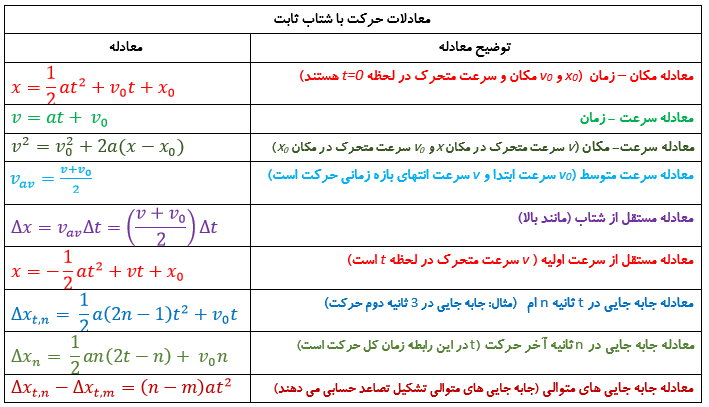
معادلات حرکت بسته به نوع سیستم و شرایط خاص آن، می‌توانند اشکال متفاوتی داشته باشند. این تفاوت‌ها به ویژه زمانی نمایان می‌شود که حرکت اجسام در شرایط گوناگون فیزیکی، مانند حرکت در مسیر مستقیم یا حرکت در مسیر منحنی، تحلیل می‌شود. برای هر نوع حرکت، معادله خاصی وجود دارد که پارامترهای مختلفی همچون سرعت، شتاب و نیرو را در نظر می‌گیرد.

در سیستم‌های مختلف، معادلات حرکت می‌توانند به شکل‌های مختلفی ارائه شوند. برای مثال، در حرکت‌های خطی، معادلات ساده‌تری وجود دارند که به راحتی می‌توانند تغییرات موقعیت جسم را با گذشت زمان توصیف کنند. در حالی که در سیستم‌های پیچیده‌تر، مانند حرکت‌های دورانی یا حرکت‌های تحت تأثیر نیروهای پیچیده‌تر، معادلات حرکتی به اشکال پیچیده‌تری در می‌آیند.

علاوه بر این، نوع نیروهای مؤثر در حرکت نیز می‌تواند تأثیر زیادی بر شکل معادلات داشته باشد. در برخی موارد، معادلات حرکت تنها با استفاده از نیروی گرانش یا کشش سطحی به دست می‌آیند، در حالی که در موارد دیگر ممکن است نیاز به در نظر گرفتن نیروهای مختلفی مانند نیروی اصطکاک، نیروهای الکترومغناطیسی یا حتی نیروهای کوانتومی باشد.

معادلات حرکت خطی و منحنی

در تحلیل حرکت اجسام، معادلات حرکت خطی و منحنی از جمله ابزارهای اصلی برای توصیف مسیر و سرعت اجسام هستند. هر کدام از این معادلات ویژگی‌ها و کاربردهای خاص خود را دارند که بسته به نوع حرکت، می‌توانند به شکل‌های مختلفی بیان شوند. حرکت خطی به جابجایی اجسام در یک خط راست اشاره دارد، در حالی که حرکت منحنی به حرکت در مسیرهایی گفته می‌شود که تغییرات جهت دارند.

معادلات حرکت خطی

در حرکت خطی، معمولاً فرض بر این است که جسم در یک راستا حرکت می‌کند و تغییرات موقعیت آن تنها در یک بعد صورت می‌گیرد. معادلات این نوع حرکت به راحتی قابل حل هستند و در بسیاری از مسائل فیزیکی و مهندسی استفاده می‌شوند. در این معادلات، معمولاً از سه پارامتر اصلی استفاده می‌شود: موقعیت، سرعت و شتاب. به‌طور کلی، معادلات حرکت خطی به دو دسته تقسیم می‌شوند:

• حرکت با شتاب ثابت: در این نوع حرکت، شتاب جسم در طول زمان تغییر نمی‌کند و معادلات حرکت به‌صورت ساده و خطی هستند.
• حرکت تحت تأثیر نیروهای متغیر: در این حالت، نیروهای وارد بر جسم با گذشت زمان تغییر می‌کنند و معادلات حرکت پیچیده‌تر می‌شوند.

معادلات حرکت منحنی

در حرکت منحنی، تغییرات جهت حرکت اجسام در هر لحظه مهم است. این نوع حرکت بیشتر در سیستم‌هایی که تحت تأثیر نیروهای مرکزی یا نیروهای تغییر مسیر قرار دارند، مشاهده می‌شود. معادلات حرکت منحنی معمولاً با در نظر گرفتن شتاب زاویه‌ای و سرعت زاویه‌ای به‌دست می‌آیند. این معادلات شامل موارد زیر هستند:

1. حرکت دایره‌ای یکنواخت: در این نوع حرکت، جسم در یک مسیر دایره‌ای ثابت حرکت می‌کند و شتاب آن همیشه در جهت مرکز دایره است.
2. حرکت دایره‌ای شتابدار: در این نوع حرکت، جسم به دلیل وجود شتاب زاویه‌ای، مسیر خود را با تغییراتی در سرعت زاویه‌ای طی می‌کند.

استفاده در طراحی سیستم‌های مکانیکی

معادلات حرکت در طراحی سیستم‌های مکانیکی ابزارهای مهمی برای تحلیل و پیش‌بینی رفتار اجسام در حین حرکت هستند. این معادلات به مهندسان و طراحان این امکان را می‌دهند که با استفاده از اصول فیزیکی و ریاضی، سیستم‌هایی با کارایی بالا و ایمنی بیشتر طراحی کنند. در این سیستم‌ها، معادلات حرکت نه تنها برای تحلیل حرکات اجسام بلکه برای محاسبه نیروها، شتاب‌ها و تغییرات انرژی نیز کاربرد دارند.

طراحی ماشین‌آلات و ربات‌ها

در طراحی ماشین‌آلات و ربات‌ها، معادلات حرکت به‌ویژه در تحلیل حرکات پیچیده مکانیکی اهمیت دارند. این معادلات به طراحان کمک می‌کنند تا مسیر حرکتی اجزای مختلف یک سیستم را پیش‌بینی کرده و نیروهای وارد بر هر بخش از ماشین را محاسبه کنند. به‌طور مثال، در طراحی ربات‌های صنعتی، حرکت دقیق و هماهنگ بخش‌های مختلف از جمله بازوها و چرخ‌ها، نیازمند استفاده از معادلات حرکت برای رسیدن به کارایی مطلوب است.

سیستم‌های تعلیق و انتقال نیرو

در سیستم‌های تعلیق خودروها و مکانیزم‌های انتقال نیرو، معادلات حرکت برای شبیه‌سازی رفتار اجسام در برابر نیروهای وارده و تحلیل پاسخ سیستم‌های پیچیده مانند فنرها، دمپرها و اتصالات استفاده می‌شوند. این معادلات به مهندسان این امکان را می‌دهند که طراحی‌های بهینه برای کاهش ارتعاشات، افزایش راحتی و کاهش مصرف انرژی داشته باشند. با مدل‌سازی دقیق حرکت و نیروها، می‌توان بهبود عملکرد سیستم‌ها را تضمین کرد.

روش‌های تحلیلی و عددی

برای حل معادلات حرکت، دو رویکرد اصلی وجود دارد: روش‌های تحلیلی و عددی. هر یک از این روش‌ها به گونه‌ای خاص به تحلیل و یافتن پاسخ معادلات حرکت می‌پردازند و بسته به پیچیدگی مسئله و نیازهای مختلف، انتخاب مناسب‌ترین روش بسیار مهم است. روش‌های تحلیلی معمولاً برای مسائل ساده‌تر که به راحتی قابل حل هستند، کاربرد دارند، در حالی که روش‌های عددی برای مسائل پیچیده‌تر و غیرخطی که حل آن‌ها به صورت تحلیلی دشوار است، استفاده می‌شوند.

روش‌های تحلیلی

در روش‌های تحلیلی، حل معادلات حرکت با استفاده از تکنیک‌های ریاضی انجام می‌شود. این روش‌ها بر اساس حل مستقیم معادلات دیفرانسیل و استفاده از فرمول‌های شناخته‌شده به نتیجه می‌رسند. از مهم‌ترین مزایای این روش می‌توان به دقت بالا و نتایج قابل‌اعتماد اشاره کرد. در بسیاری از موارد، معادلات حرکت به‌طور کامل و با دقت دقیق قابل حل هستند و نتایج آن‌ها به صورت نمادین یا بسته‌ای از معادلات به‌دست می‌آید. این روش به‌ویژه برای مسائل ساده‌تری که در آن‌ها تغییرات غیرخطی یا پیچیدگی‌های زیاد وجود ندارد، مناسب است.

روش‌های عددی

در مواردی که معادلات حرکت پیچیده‌تر و غیرخطی هستند یا نیاز به دقت بالا در سیستم‌های بزرگ وجود دارد، روش‌های عددی به کار می‌روند. در این روش‌ها، معادلات حرکت به‌طور عددی حل شده و نتیجه به صورت تقریبی به دست می‌آید. این روش‌ها از الگوریتم‌های خاصی برای تقسیم زمان و فضای مسئله به بخش‌های کوچک‌تر استفاده می‌کنند و به تدریج نتیجه را محاسبه می‌کنند. مهم‌ترین مزیت این روش‌ها قابلیت حل مسائل پیچیده و شرایط غیرخطی است، اما نتیجه به‌دست‌آمده ممکن است دارای خطاهای عددی باشد.