همبستگی پیرسون چه چیزی را نشان می دهد؟

• امیرروکا
• 2024-11-20

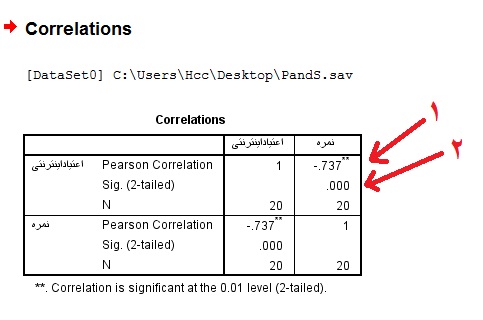
همبستگی یکی از ابزارهای اصلی در تحلیل داده‌ها است که برای بررسی رابطه میان متغیرها به کار می‌رود. در این میان، همبستگی پیرسون یکی از رایج‌ترین روش‌هاست که به طور گسترده در زمینه‌های مختلف علمی مورد استفاده قرار می‌گیرد.

همبستگی پیرسون به ما کمک می‌کند تا شدت و جهت رابطه بین دو متغیر را اندازه‌گیری کنیم. این ابزار به‌ویژه در تحلیل داده‌های عددی و درک روابط میان متغیرهایی که به صورت خطی به یکدیگر مرتبط هستند، کاربرد دارد.

در این مقاله، علاوه بر معرفی این مفهوم، به بررسی کاربردها، تفاوت آن با دیگر روش‌ها و محدودیت‌های استفاده از آن پرداخته خواهد شد. هدف این است که دیدگاه روشنی درباره نقش همبستگی پیرسون در تحلیل داده‌ها ارائه شود.

همبستگی پیرسون چیست و چگونه محاسبه می‌شود؟

بررسی روابط میان متغیرها یکی از ابزارهای مهم در تحلیل داده‌ها است. همبستگی پیرسون روشی شناخته‌شده برای ارزیابی میزان ارتباط میان دو متغیر است که بر اساس تغییرات همزمان آنها عمل می‌کند. این روش به‌ویژه زمانی مفید است که بخواهیم شدت و جهت این ارتباط را به‌طور کمی اندازه‌گیری کنیم.

برای محاسبه همبستگی پیرسون، از یک فرمول خاص استفاده می‌شود که به بررسی تغییرات نسبی دو متغیر نسبت به میانگین آنها می‌پردازد. این محاسبه نتیجه‌ای بین -۱ تا ۱ ارائه می‌دهد، که مقدار مثبت نشان‌دهنده رابطه مستقیم، مقدار منفی نشان‌دهنده رابطه معکوس و مقدار صفر بیانگر نبود رابطه است.

این روش به دلیل دقت بالا و سادگی محاسبه، در علوم مختلفی مانند آمار، روانشناسی و اقتصاد به طور گسترده استفاده می‌شود. با این حال، درک محدودیت‌های آن برای جلوگیری از تفسیر اشتباه ضروری است.

کاربردهای عملی همبستگی پیرسون در علم داده

در تحلیل داده‌ها، شناسایی روابط میان متغیرها نقشی کلیدی در استخراج اطلاعات ارزشمند دارد. همبستگی پیرسون یکی از ابزارهای قابل اعتماد است که به تحلیل‌گران کمک می‌کند تا الگوهای ارتباطی را در داده‌ها کشف کنند و تصمیم‌گیری‌های مبتنی بر داده را بهبود بخشند.

تحلیل پیش‌بینی در مدل‌های آماری

یکی از کاربردهای اصلی همبستگی پیرسون در ایجاد مدل‌های پیش‌بینی است. با استفاده از این روش، می‌توان متغیرهایی که تأثیر بیشتری بر نتایج مدل دارند شناسایی کرد و دقت پیش‌بینی‌ها را افزایش داد. این کاربرد در زمینه‌هایی مانند پیش‌بینی فروش، تحلیل رفتار مشتریان و تشخیص بیماری‌ها بسیار مفید است.

کشف روابط در داده‌های پیچیده

در داده‌های بزرگ و پیچیده، استفاده از همبستگی پیرسون می‌تواند به کشف ارتباطات ناشناخته کمک کند. این روش به‌ویژه در تحلیل شبکه‌های اجتماعی، داده‌های ژنتیکی و مطالعات بازار برای شناسایی روندها و همبستگی‌های مهم به کار می‌رود.

تفاوت همبستگی پیرسون و دیگر روش‌ها

برای تحلیل روابط میان متغیرها، روش‌های مختلفی در دسترس هستند که هر کدام بر اساس نوع داده و اهداف تحلیل انتخاب می‌شوند. همبستگی پیرسون در کنار این روش‌ها قرار دارد و ویژگی‌های خاصی دارد که آن را از دیگر تکنیک‌ها متمایز می‌کند.

مقایسه با همبستگی اسپیرمن

• همبستگی پیرسون برای متغیرهایی مناسب است که رابطه‌ای خطی دارند، در حالی که اسپیرمن به روابط غیرخطی و رتبه‌ای توجه می‌کند.
• در صورتی که داده‌ها دارای نقاط پرت باشند، اسپیرمن نسبت به پیرسون مقاوم‌تر است.

تفاوت با کوواریانس

1. کوواریانس شدت رابطه را بدون مقیاس مشخص نشان می‌دهد، اما همبستگی پیرسون مقدار استانداردشده‌ای بین -۱ و ۱ ارائه می‌دهد.
2. کوواریانس تنها جهت و شدت کلی رابطه را ارائه می‌دهد، در حالی که پیرسون تفسیر دقیقی از رابطه متناسب بین متغیرها ارائه می‌دهد.

در انتخاب روش مناسب، توجه به نوع داده و هدف تحلیل اهمیت زیادی دارد. همبستگی پیرسون زمانی بهترین انتخاب است که داده‌ها عددی و رابطه میان متغیرها خطی باشد.

محدودیت‌های استفاده از همبستگی پیرسون

اگرچه همبستگی پیرسون ابزاری قدرتمند برای تحلیل روابط میان متغیرها است، اما این روش در شرایط خاص با محدودیت‌هایی مواجه می‌شود. شناخت این محدودیت‌ها برای تفسیر صحیح نتایج و جلوگیری از برداشت‌های اشتباه ضروری است.

حساسیت به نقاط پرت

همبستگی پیرسون به شدت تحت تأثیر نقاط پرت قرار می‌گیرد. این نقاط می‌توانند مقدار همبستگی را به صورت غیرواقعی افزایش یا کاهش دهند و در نتیجه تحلیل را گمراه کنند. برای مقابله با این مشکل، استفاده از روش‌های مقاوم مانند همبستگی اسپیرمن توصیه می‌شود.

وابستگی به رابطه خطی

یکی دیگر از محدودیت‌های این روش، نیاز به وجود رابطه خطی میان متغیرها است. در صورت وجود روابط غیرخطی، مقدار همبستگی پیرسون نمی‌تواند به درستی ارتباط واقعی را نشان دهد. در چنین مواردی، روش‌های جایگزین مناسب‌تر خواهند بود.

در مجموع، هنگام استفاده از همبستگی پیرسون باید به این محدودیت‌ها توجه کرد تا تحلیل‌ها دقیق‌تر و نتایج قابل اعتمادتر باشند.